Types of Function ?

There are five types of function :

(1) One-to-One function or One-One function or Injective function

(2) Many-to-One function or Many-One function

(3) Onto function or Surjective function

(4) Into function

(5) Bijective function

One-to-One function or One-one function

A function 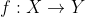   is said to be one-to-one function, if image of distinct elements of  X
are distinct under  f . In other words, functions for which each element of the  set X   is
mapped to a different element of the  set Y   are said to be one-to-one function     

                                   

                                                        The domain is  { A , B , C }

                                                       The co-domain is { 1 , 2 , 3 , 4 }

                                                       The range is { 1 , 2  , 3 }

Many-to-one function or Many-one function

A function 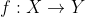   is said to be many-to-one function, if more than one elements of  X
are mapped to the same element of  Y .  In other words, a function can map more than one
element of the  set X  to the same element of the  set Y  .  Such a type of function is said to be
many-to-one function.      

                                         

                                                          The domain is  { A , B , C }

                                                         The co-domain is { 1 , 2 , 3 , 4 }

                                                         The range is { 1 , 4 }

Onto function or Surjective function

A function    is said to be Onto function, if every element of the  set Y  is the 

image of at least one element of   set X   i.e, if their is no unpaired element in the  set Y  then

we say that  function  f  maps the  set X  onto  set Y . Such a function is known as

Onto function.        

                                                

                                                         The domain is { a , b , c , d }

                                                           The co-domain is { 1 , 2 , 3 }

                                                           The range is { 1 , 2 , 3 }

Note:  In Onto function   Co-domain = range  and  range ⊆ Co-domain.

Into function

A function    is said to be Into function, if their is unpaired element in the  set Y

then we say that  function  f  maps the  set X  Into  set Y . Such a function is known as

Into function.  

                                              

                                                         The domain is { a , b , c }

                                                           The co-domain is { 1 , 2 , 3 , 4 }

                                                           The range is { 1 , 3 , 4 }

Note:  In Into function   range ⊂ Co-domain.

Bijective Function

A function which is both One-one function and Onto function  is said to be a Bijective

function.

                                         

                                                           The domain is { a , b , c }

                                                           The co-domain is { 1 , 2 }

                                                           The range is { 1 , 2 }