Reflexive Relation | Symmetric Relation | Transitive Relation

Reflexive Relation

A relation R on a set A is said to be reflexive if every element of A is related to itself.

Thus,    .
Note : A relation is not reflexive if their exists an element   such that  (a,a)∉R .

For example : Let   A = { 1 , 2 , 3 }  be a set. Then

                            is a reflexive relation on  A.
             but,      is not a reflexive relation on  A , 
                         because  2 ∈ A but  (2,2) ∉ R .
Note : For reflexive relation doublet of every element of a given set should be present .

Symmetric Relation
A relation R on a set A is said to be symmetric relation if  (a,b)∈R  (b,a)∈R 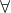   (a,b)∈A
i.e.  aRb  bRa  for all  a , b ∈ A  .

For example : Let   A = { 1 , 2 , 3 , 4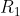 }  and   and 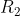   be relations on  A  given by
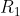                           = { (1,3) , (1,4) , (3,1) , (2,2) , (4,1) }
          and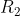         = { (1,1) , (2,2) , (3,3) , (1,3) }

In above relations :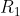    is symmetric on  A  because (a,b) ∈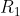    (b,a) ∈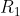 
                      but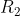         is not symmetric on  A  because (1,3) ∈  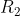 but  (3,1) ∉  .
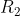Note : A reflexive relation on a set A  is not necessarily symmetric. 
            e.g:  the relation  R = {(1,1),(2,2),(3,3),(1,3)}  is a reflexive on  set A = {1,2,3} 
                     but it is not symmetric.

Transitive Relation
Let  A  be any set. A relation  R on A  is said to be transitive relation if 
(a,b) ∈ R  and  (b,c) ∈ R  (a,c) ∈ R  for all  a,b,c ∈ A .
i.e., aRb and bRc  aRc  for all   a,b,c ∈ A .

For example : On the set N  of natural numbers, the relation R defined by  xRy .
                      'x  is less than  y' , is transitive , because for any  x,y,z ∈ N
                           x < y  and  y < z    x < z
                  i.e.,  xRy  and  yRz    xRz