Minors and Co-factors

The value of determinant of square matrix of order 3 or more is defined in terms of

Co-factors of ts elements.

Let $A=[a_{ij}]$ be a square matrix of order n .
∴ $|A|=|a_{ij}|$
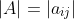
The determinant obtained by removing its ith row and jth column in |A| is denoted by
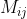$M_{ij}$ is called the minor of the element 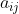$a_{ij}$ . The minor 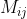$M_{ij}$ of the element 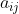$a_{ij}$ is called
a minor of the matrix A and also of the determinant |A| .
Thus, we see that, the determinant obtained from a determinant by omitting the row
and the column in which a particular element lies is the minor of that element.

For example : if

$|A|=\begin{vmatrix} 4 & 3 & 8\\ 6 & 7 & 5\\ 3 & 1 & 2 \end{vmatrix} \ , \ then$

$M_{12}=minor \ of \ a_{12} \ (=3)=\begin{vmatrix} 6 & 5\\ 3 & 2 \end{vmatrix}=12-15=-3$

$M_{31}=minor \ of \ a_{31} \ (=3)=\begin{vmatrix} 3 & 8\\ 7 & 5 \end{vmatrix}=18-56=-41$
If   $M_{ij}$ is the minor of   $a_{ij}$ , then $(-1)^{i+j} M_{ij}$ is called the co-factor of   $a_{ij}$ and is denoted
by   $A_{ij}$ .
∴ co-factor of $a_{ij}=A_{ij}=(-1)^{i+j} M_{ij}$
In above example,

$A_{12}=(-1)^{1+2} M_{12} = (-1)(-3) = 3$

$A_{31}=(-1)^{3+1} M_{31} = (1)(-41) = -41$

Remark : $(-1)^{i+j}$ is 1 or -1 according as i + j is even or odd.
∴ $A_{ij}$ and $M_{ij}$ coincides if i + j is even. And if i + j is odd then we have $A_{ij}= \ - \ M_{ij}$ .

Sharma Academy

Search This Blog

Minors and Co-factors

Comments

Post a Comment